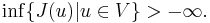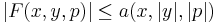Direct method in the calculus of variations
In the calculus of variations, a topic in mathematics, the direct method is a general method for constructing a proof of the existence of a minimizer for a given functional,[1] introduced by Zaremba and David Hilbert around 1900. The method relies on methods of functional analysis and topology. As well as being used to prove the existence of a solution, direct methods may be used to compute the solution to desired accuracy.[2]
Contents |
The method
The calculus of variations deals with functionals 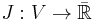 , where
, where  is some function space and
is some function space and 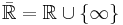 . The main interest of the subject is to find minimizers for such functionals, that is, functions
. The main interest of the subject is to find minimizers for such functionals, that is, functions 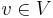 such that:
such that: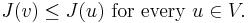
The standard tool for obtaining necessary conditions for a function to be a minimizer is the Euler–Lagrange equation. But seeking a minimizer amongst functions satisfying these may lead to false conclusions if the existence of a minimizer is not established beforehand.
The functional  must be bounded from below to have a minimizer. This means
must be bounded from below to have a minimizer. This means
It is not enough to know that a minimizer exists, but it shows the existence of a minimizing sequence, that is, a sequence 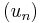 in
in  such that
such that 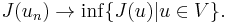
The direct method may broken into the following steps
- Take a minimizing sequence
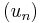 for
for  .
. - Show that
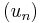 admits some subsequence
admits some subsequence 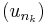 , that converges to a
, that converges to a 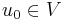 with respect to a topology
with respect to a topology  on
on  .
. - Show that
 is sequentially lower semi-continuous with respect to the topology
is sequentially lower semi-continuous with respect to the topology  .
.
To see that this shows the existence of a minimizer, consider the following characterization of sequentially lower-semicontinuous functions.
- The function
 is sequentially lower-semicontinuous if
is sequentially lower-semicontinuous if
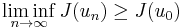 for any convergent sequence
for any convergent sequence 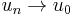 in
in  .
.
The conclusions follows from
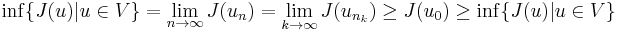 ,
,
in other words
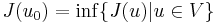 .
.
Details
Banach spaces
The direct method may often be applied with success when the space  is a subset of a reflexive Banach space
is a subset of a reflexive Banach space 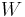 . In this case the Banach–Alaoglu theorem implies, that any bounded sequence
. In this case the Banach–Alaoglu theorem implies, that any bounded sequence 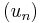 in
in  has a subsequence that converges to some
has a subsequence that converges to some 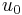 in
in 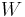 with respect to the weak topology. If
with respect to the weak topology. If  is sequentially closed in
is sequentially closed in 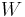 , so that
, so that 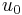 is in
is in  , the direct method may be applied to a functional
, the direct method may be applied to a functional 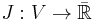 by showing
by showing
 is bounded from below,
is bounded from below,- any minimizing sequence for
 is bounded, and
is bounded, and  is weakly sequentially lower semi-continuous, i.e., for any weakly convergent sequence
is weakly sequentially lower semi-continuous, i.e., for any weakly convergent sequence 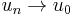 it holds that
it holds that 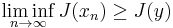 .
.
The second part is usually accomplished by showing that  admits some growth condition. An example is
admits some growth condition. An example is
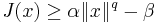 for some
for some 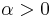 ,
, 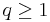 and
and 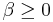 .
.
A functional with this property is sometimes called coercive. Showing sequential lower semi-continuity is usually the most difficult part when applying the direct method. See below for some theorems for a general class of functionals.
Sobolev spaces
The typical functional in the calculus of variations is an integral of the form
where  is a subset of
is a subset of 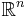 and
and  is a real-valued function on
is a real-valued function on 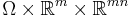 . The argument of
. The argument of  is a differentiable function
is a differentiable function  , and its Jacobian
, and its Jacobian 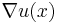 is identified with a
is identified with a 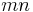 -vector.
-vector.
When deriving the Euler–Lagrange equation, the common approach is to assume  has a
has a 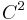 boundary and let the domain of definition for
boundary and let the domain of definition for  be
be 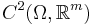 . This space is a Banach space when endowed with the supremum norm, but it is not reflexive. When applying the direct method, the functional is usually defined on a Sobolev space
. This space is a Banach space when endowed with the supremum norm, but it is not reflexive. When applying the direct method, the functional is usually defined on a Sobolev space 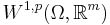 with
with 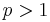 , which is a reflexive Banach spaces. The derivatives of
, which is a reflexive Banach spaces. The derivatives of  in the formula for
in the formula for  must then be taken as weak derivatives. The next section presents two theorems regarding weak sequential lower semi-continuity of functionals of the above type.
must then be taken as weak derivatives. The next section presents two theorems regarding weak sequential lower semi-continuity of functionals of the above type.
Sequential lower semi-continuity of integrals
As many functionals in the calculus of variations are of the form
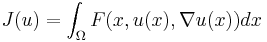 ,
,
where 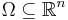 is open, theorems characterizing functions
is open, theorems characterizing functions  for which
for which  is weakly sequentially lower-semicontinuous in
is weakly sequentially lower-semicontinuous in 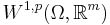 is of great importance.
is of great importance.
In general we have the following[3]
- Assume that
 is a function such that
is a function such that
- The function
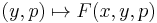 is continuous for almost every
is continuous for almost every 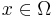 ,
, - the function
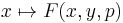 is measurable for every
is measurable for every 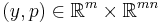 , and
, and 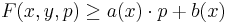 for a fixed
for a fixed 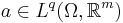 where
where 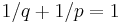 , a fixed
, a fixed 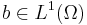 , for a.e.
, for a.e. 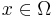 and every
and every 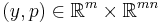 (here
(here 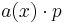 means the inner product of
means the inner product of 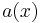 and
and  in
in 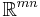 ).
).
- The function
- The following holds. If the function
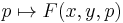 is convex for a.e.
is convex for a.e. 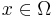 and every
and every 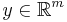 ,
, - then
 is sequentially weakly lower semi-continuous.
is sequentially weakly lower semi-continuous.
When 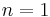 or
or 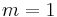 the following converse-like theorem holds[4]
the following converse-like theorem holds[4]
- Assume that
 is continuous and satisfies
is continuous and satisfies
- for every
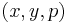 , and a fixed function
, and a fixed function 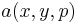 increasing in
increasing in  and
and  , and locally integrable in
, and locally integrable in  . It then holds, if
. It then holds, if  is sequentially weakly lower semi-continuous, then for any given
is sequentially weakly lower semi-continuous, then for any given 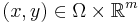 the function
the function 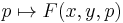 is convex.
is convex.
In conclusion, when 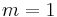 or
or 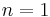 , the functional
, the functional  , assuming reasonable growth and boundedness on
, assuming reasonable growth and boundedness on  , is weakly sequentially lower semi-continuous if, and only if, the function
, is weakly sequentially lower semi-continuous if, and only if, the function 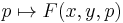 is convex. If both
is convex. If both  and
and  are greater than 1, it is possible to weaken the necessity of convexity to generalizations of convexity, namely polyconvexity and quasiconvexity.[5]
are greater than 1, it is possible to weaken the necessity of convexity to generalizations of convexity, namely polyconvexity and quasiconvexity.[5]
Notes
References and further reading
- Dacorogna, Bernard (1989). Direct Methods in the Calculus of Variations. Springer-Verlag. ISBN 0-387-50491-5.
- Fonseca, Irene; Giovanni Leoni (2007). Modern Methods in the Calculus of Variations:
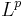 Spaces. Springer. ISBN 978-0-387-35784-3.
Spaces. Springer. ISBN 978-0-387-35784-3.